Le problème de Monty Hall

Présentation du jeu

Monty Hall est le présentateur d'une émission télévisée américaine des années 60-70. Dans cette émission, les candidats se voyaient proposer un choix à l'aveugle parmi trois portes fermées :

  • Derrière l'une des portes se trouve une voiture qui récompense le candidat gagnant
  • Derrière les deux autres, se trouvent deux chèvres qui désignent alors le candidat comme perdant.
Le choix se déroule en deux temps :
  • Le candidat commence par choisir une des portes
  • Puis Monty Hall ouvre une des deux portes perdantes pour la retirer
  • Le candidat a alors la possibilité de changer d'avis ou de rester fidèle à son premier choix

Les candidats sont divisés entre :
  • ceux qui pensent qu'il faut toujours rester sur sa première impression
  • ceux qui doutent au moment du choix et changent d'avis

Essayer le jeu

Vous pouvez essayer les deux stratégies afin de vous convaincre si une des deux est plus efficace...

Exercice : Arbre de probabilités

Le but de l'exercice est de calculer la probabilité de gagner pour chaque stratégie : changer ou garder son avis.

1 Construire un arbre de probabilité représentant les deux étapes successives du jeu :
  1. Le choix aveugle du candidat parmi les 3 portes : on notera \(C_1\) la première chèvre, \(C_2\) la deuxième chèvre, \(V\) la voiture
  2. Le choix du présentatuer Monty Hall de se débarrasser d'une chèvre : on notera \(C_1\) la première chèvre, \(C_2\) la deuxième chèvre
Attention, si sans le savoir, le candidat a choisi une chèvre, Monty Hall ne peut pas choisir d'enlever cette même chèvre.

Cliquer pour dévoiler la réponse
Masquer

2 A droite de l'arbre, pour chaque issue possible, écrire ce qu'il reste derrière les portes (si il reste la voiture et la première chèvre, on écrire \((V ; C_1)\)). Calculer la probabilité pour chaque issue sous forme de fraction.

Cliquer pour dévoiler la réponse
Masquer

3 On choisit la stratégie qui consiste à garder son avis au deuxième choix :
a Quelles sont les issues de l'arbre qui donnent le candidat gagnant ?
b Calculer la probabilité de gagner.
Pour obtenir la probabilité de gagner, il faut sommer les issues gagnantes
4 On choisit la stratégie qui consiste à changer d'avis au deuxième choix :
a Quelles sont les issues de l'arbre qui donnent le candidat gagnant ?
b Calculer la probabilité de gagner.

Cliquer pour dévoiler la réponse
Masquer

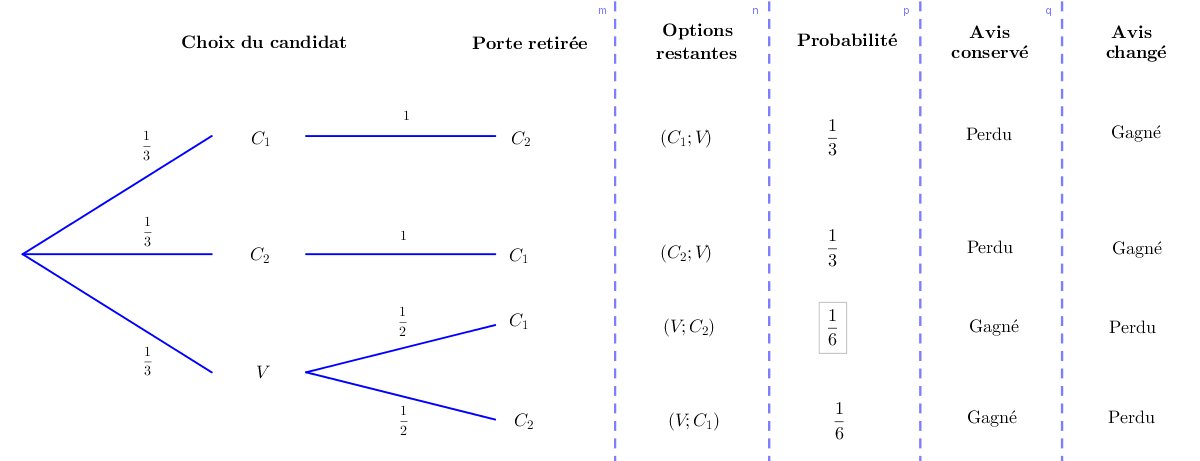
Stratégie "Avis conservé" :

On gagne seulement dans les deux derniers cas \((V;C_2)\) ou \((V;C_1)\). La probabilité de gagner vaut : $$ p (\text{succés}) = \frac{1}{6} + \frac{1}{6} = \frac{2}{6} = \frac{1}{3} $$

Stratégie "changer d'avis" :

On gagne seulement dans les deux premiers cas \((C_1;V)\) ou \((C_2;V)\). La probabilité de gagner vaut : $$ p (\text{succés}) = \frac{1}{3} + \frac{1}{3} = \frac{2}{3} $$

5 Les deux stratégies se valent-elles ?

Cliquer pour dévoiler la réponse
Masquer
La stratégie qui consiste à changer d'avis est la meilleure. Sa probabilité de succés est deux fois plus importante que lorsque le candidat choisis de rester sur son premier choix.

Le problème de Monthy Hall fait partie de ces jeux changés ou abandonnés après que des mathématiciens l'ont étudié. Un autre exemple connu est celui du jeu de cartes le "black jack" : un film, plus ou moins fidèle, Las Vegas 21 raconte comment des mathématiciens ont pu gagner contre de nombreux casinos dans le monde...

Si ici les probabilités ont mis en évidence un déséquilibre innocent dans les règles d'un jeu télévisé, elles peuvent aussi être utilisées pour dévoiler des arnaques ou des abus de "faux-magiciens". Cette démarche s'appelle la zététique.